In-memory dictionary

Our journey to understand persistent memory begins with building an in-memory dictionary. One of the reasons we would like to begin with building an in-memory dictionary is to understand the transition from an in-memory to a persistent dictionary, and what it takes to make an in-memory data structure work with persistent memory.

The overall idea

As a part of this article, we will be building an in-memory dictionary that supports the following methods:

add(word) that adds a new word into the dictionary,
contains(word) that specifies if the given word is present in the dictionary,
containsPrefix(prefix) that specifies if there is any word beginning with the given prefix.

Choosing a data structure

A data structure is a particular way of organizing data so that it can be used efficiently. Data structures determine the efficiency and complexity of various operations in our solution.

One of the first things that we would like to do is to identify the data structure for building the dictionary. Here are a couple of the most important options:

HashMap
- Optimized for add and contains operations.
- Requires iterating through all the words to identify if there is any word beginning with the given prefix.
Trie
- Efficient structure for retrieval of information. With Trie, addition and search complexity is O(word length).
- Allows operations like containsPrefix to be done in O(prefix length) time.

We could have also mentioned Compressed Trie but to keep the article simple, we will use Trie for representing the dictionary, but to better understand it, we will start with a brief introduction to its predecessor.

A quick introduction to Tree

Tree is a data structure that is used to represent hierarchical data.

Tree

For example, the above tree shows the organizational hierarchy of a company. Here, John is the CEO of the company. Rahul and Carl directly report to John. Carl further has two direct reportees named Thomas and Mark.

Some of the key points of the tree data structure are:

A tree data structure is defined as a collection of objects known as nodes that are linked together to represent or simulate hierarchy
A tree data structure is non-linear
The topmost node is known as a root node
Each node contains some data and may contain link(s) or reference(s) to other nodes that can be called children nodes
Nodes without any children are called leaf nodes
Rest of the nodes are called non-leaf nodes

Understanding Trie

Trie is a tree-like data structure where every node represents a single character of a group of words stored by this trie. Each trie node also contains a boolean flag to state if the node represents the end of the word.

Our representation of the trie node will be:

class TrieNode {
    private:
    bool endOfWord;
    std::map<char, TrieNode*> nodeByCharacter;
}

Let's see a couple of words and understand how TrieNode(s) are being used.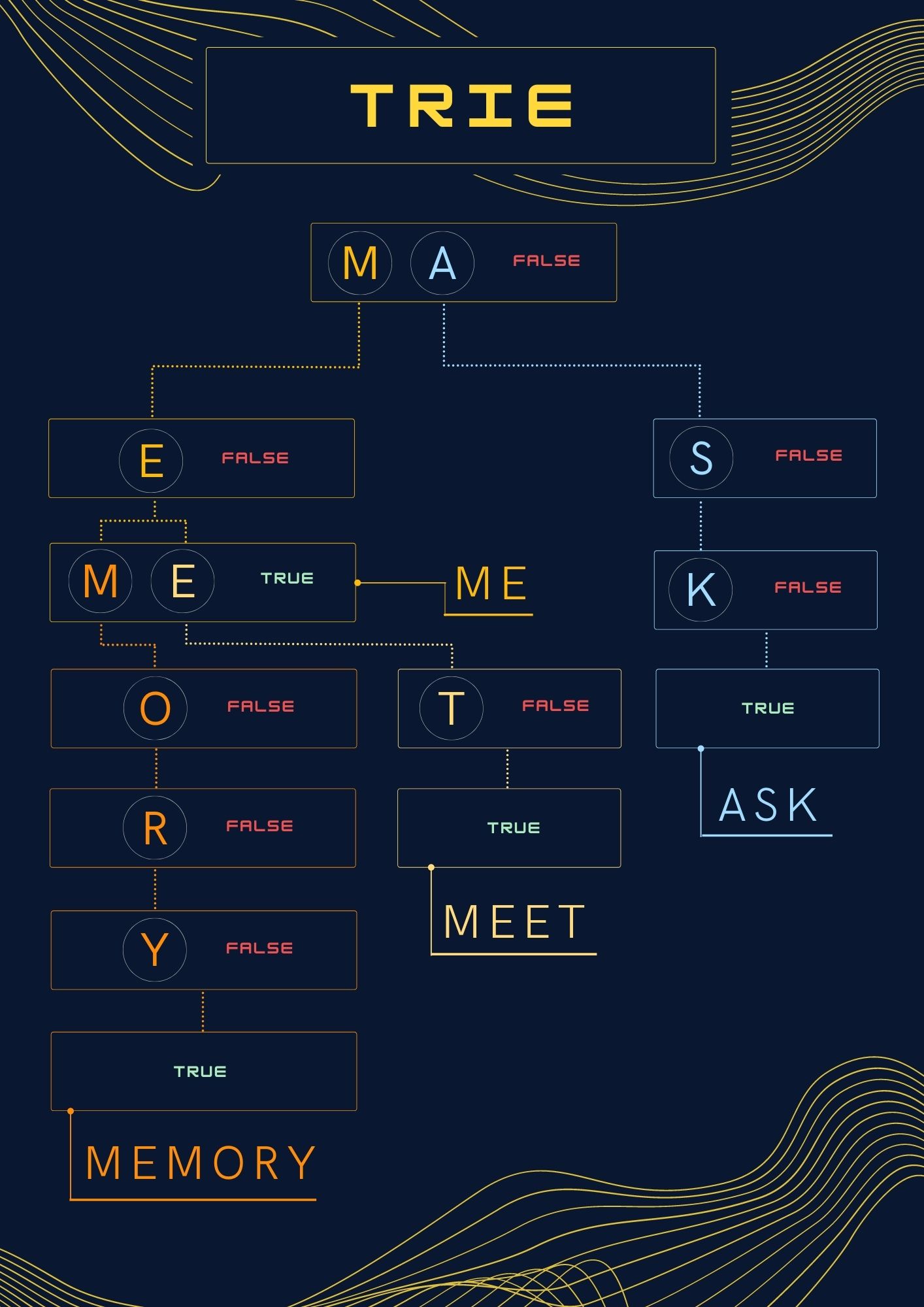

Words built using TrieNodes

The above diagram represents me, memory, meet, and ask words.

The diagram illustrates that each node contains a mapping between a character and a pointer to the next node in a word. The diagram also represents overlapping nodes between the words me, memory, and meet.

Let's try and add the word ask in an empty trie.

We start with the root node and check if it contains the letter a. Since a is not present in the root node, we add it to the root node with a pointer pointing to a newly created node. We then jump to the newly created node.

Now we check if the newly created node contains the letter s. Since s is not present in the node, we add it to the node with a pointer pointing to another new node. We jump to the new node and repeat the same process for the letter k.

Once we are done with the entire word, we mark the endOfWord on the final node as true.

Let's try and find the word ask in the above trie.

To do this, we start with the root node and check if it contains the letter a. Since the root node contains a, we jump to the node pointed to by this letter.

Now we check if the node contains the letter s. Since s is present in the node, we jump to the node pointed to by this letter and repeat the same process for the letter k.

Once we are done with the entire word, we check the endOfWord on the final node. If it is true, the word exists in the dictionary else it does not.

Building an in-memory dictionary

Our dictionary will be represented by a class called Trie which contains a pointer to the root TrieNode. Each TrieNode contains two fields:

a boolean flag to indicate the end of a word
a mapping between a character of a word and a pointer to the next node

Our dictionary supports three behaviors: add, contains and containsPrefix.

namespace dictionary {
    namespace inmem {
        class Trie {
            private:
            TrieNode* root;

            public:
            void add(string word);
            bool contains(string word);
            bool containsPrefix(string prefix);    
        }

        class TrieNode {
            private:
            bool endOfWord;
            std::map<char, TrieNode*> nodeByCharacter;

            public:
            void add(string word);
            bool contains(string word);
            bool containsPrefix(string prefix); 
        }
    }
}

Adding tests for `add` and `contains`

Let's add a couple of tests for adding words and checking if the dictionary contains a given word.

#include <gtest/gtest.h>
#include "../src/Trie.h"

using namespace dictionary::inmem;

TEST(InMemoryDictionary, ContainsAnAddedWord) {
    Trie* dictionary = new Trie();
    dictionary -> add("meet");
    dictionary -> add("memory");

    ASSERT_TRUE(dictionary -> contains("memory"));
}

TEST(InMemoryDictionary, DoesNotContainAWord) {
    Trie* dictionary = new Trie();
    dictionary -> add("meet");
    dictionary -> add("memory");

    ASSERT_FALSE(dictionary -> contains("market"));
}

Let's start with the add method. The overall idea behind add can be summarized as:

Start with the root node as the current node
For every character in the user-provided word:
- check if the current node contains the character
- if the character is present, move the current pointer to the node pointed to by the character
- else create an empty node and add the character in the current node's map with a pointer to the newly created empty node
- move the current pointer
At the end of the iteration set the endOfWord to true on the current node

This is how the above approach can be implemented in C++:

void Trie::add(std::string word) {
    this -> root -> add(word);
}

void TrieNode::add(std::string word) {
    TrieNode* current = this;
    for (auto &ch : word) {
        std::map<char, TrieNode*>::iterator iterator = current -> nodeByCharacter.find(ch);
        if (iterator == current -> nodeByCharacter.end()) { 
            //current character is not present, so insert it
            current -> nodeByCharacter.insert(std::make_pair(ch, new TrieNode()));
        } 
        current = current -> nodeByCharacter.find(ch) -> second;
    }
    current -> endOfWord = true;
}

With add done, let's code contains. The overall idea behind contains can be summarized as:

Start with the root node as the current node
For every character in the user-provided word:
- check if the current node contains the character
- if the character is not present, return false
- else move the current pointer to the node pointed to by the character
At the end of the iteration, ensure endOfWord on the current node is true

This is how the above approach can be implemented in C++:

bool Trie::contains(std::string word) {
    return this -> root -> contains(word);
}

bool TrieNode::contains(std::string word) {
    TrieNode* current = this;
    for (auto &ch : word) {
        std::map<char, TrieNode*>::iterator iterator = current -> nodeByCharacter.find(ch);
        if (iterator == current -> nodeByCharacter.end()) { 
            //current character is not present, so return
            return false;
        } 
        current = iterator -> second;
    }
    return current -> endOfWord == true;
}

Adding tests for `containsPrefix`

Let's add tests for checking if the dictionary contains any word by a given prefix.

#include <gtest/gtest.h>
#include "../src/Trie.h"

using namespace dictionary::inmem;

TEST(InMemoryDictionary, ContainsAWordByPrefix) {
    Trie* dictionary = new Trie();
    dictionary -> add("meet");
    dictionary -> add("memory");

    ASSERT_TRUE(dictionary -> containsPrefix("me"));
}

TEST(InMemoryDictionary, DoesNotContainAWordByPrefix) {
    Trie* dictionary = new Trie();
    dictionary -> add("meet");
    dictionary -> add("memory");

    ASSERT_FALSE(dictionary -> containsPrefix("met"));
}

Let's add containsPrefix. The overall idea behind containsPrefix can be summarized as:

Start with the root node as the current node
For every character in the user-provided word:
- check if the current node contains the character
- if the character is not present, return false
- else move the current pointer to the node pointed to by the character
At the end of the iteration just return true. Here, we do not need to check endOfWord because we are only interested in checking if there is a word with a prefix

This is how the above approach can be implemented in C++:

bool Trie::containsPrefix(std::string prefix) {
    return this -> root -> containsPrefix(prefix);
}

bool TrieNode::containsPrefix(std::string prefix) {
    TrieNode* current = this;
    for (auto &ch : prefix) {
        std::map<char, TrieNode*>::iterator iterator = current -> nodeByCharacter.find(ch);
        if (iterator == current -> nodeByCharacter.end()) { 
            //current character is not present, so return
            return false;
        } 
        current = iterator -> second;
    }
    return true;
}

Note there is duplication between contains and containsPrefix, but I will leave it as is for this article.

Conclusion

Let's summarize.

Our dictionary is built using Trie which is capable of adding words and searching words or words with a prefix in Big O(word length) / Big O(prefix length) time complexity.
This dictionary is in-memory and volatile. Since the dictionary is in-memory, we get the minimum latency while accessing the nodes.
The idea going forward is to convert this in-memory dictionary to a persistent one. It will be great if we can make the same in-memory data structure persistent with minimal changes.
To make the same in-memory data structure persistent with minimal changes, we will need persistent storage which is byte-addressable.

Code

Code for this article is available here.

References

Tree data structure

In-memory dictionary

The overall idea

Choosing a data structure

A quick introduction to Tree

Understanding Trie

Building an in-memory dictionary

Adding tests for `add` and `contains`

Adding tests for `containsPrefix`

Conclusion

Code

References

The author:

Reviewers:

Comments

In-memory dictionary

The overall idea

Choosing a data structure

A quick introduction to Tree

Understanding Trie

Building an in-memory dictionary

Adding tests for add and contains

Adding tests for containsPrefix

Conclusion

Code

References

The author:

Reviewers:

Comments

Adding tests for `add` and `contains`

Adding tests for `containsPrefix`